Построение частотных характеристик соединений типовых звеньев систем управления
Для анализа и синтеза СУ широко используются частотные характеристики. Частотная область обладает высокой информативностью в плане выявления зависимости свойств и показателей качества СУ от операторов отдельных звеньев и значений их параметров.В 2.5 приведена типовая структура одноконтурной СУ с единичной отрицательной обратной связью. Будем считать, что прямой канал передачи управляющего воздействия образован последовательным соединением типовых звеньев, рассмотренных в разд. 3. Ряд важных свойств замкнутых СУ может быть выявлен при анализе и сформирован при синтезе по частотным характеристикам разомкнутых систем, то есть по оператору прямого канала без обратной связи.
Целью раздела является описание процесса построения ЧХ СУ без использования компьютера, так как это позволяет установить влияние оператора каждого звена на вид ЧХ и, в конечном счете, на свойства СУ.
4.1. Логарифмические частотные характеристики
последовательного соединения типовых звеньев
Рассмотрим последовательное соединение нескольких звеньев, операторы которых заданы передаточными функциями. Как сказано в 2.5, ПФ такого соединения равна произведению ПФ звеньев.
Построение логарифмических ЧХ соединения основано на следующих двух положениях.
1. Используется то обстоятельство, что логарифм произведения равен сумме логарифмов сомножителей. С учетом того, что ПФ звеньев являются комплексными дробно-рациональными функциями, отдельно ЛАЧХ разомкнутой системы есть сумма ЛАЧХ звеньев соединения; ЛФЧХ разомкнутой системы также есть сумма ЛФЧХ отдельных звеньев.
2. По асимптотическим ЛАХ отдельных звеньев может быть построена асимптотическая ЛАХ системы, а уточненная ЛАХ системы может быть получена путем учета поправок. При этом необходимо заметить, что в зависимости от решаемой задачи учет всех поправок может и не понадобится.
Построим частотные характеристики СУ, структурная схема которой представлена на рис. 4.1.
 |
Рис. 4.1
Прямой канал передачи управляющего воздействия представляет собой последовательное соединение типовых звеньев: пропорциональное W1(s) = K1 = 40, интегрирующее W2(s) = K2/s = 0.2/s, два апериодических звена W3(s) = K3/(T1s+1) = 5/(s+1), W4(s) = K4/(T2s+1) = 0.25/(s+1). В данном случае апериодические звенья имеют совпадающие постоянные времени T1 = T2 = 1 с.
Построение ЛАХ. На рис. 4.2. построены асимптотические ЛАХ Li(w), i =1, 2, 3, 4 отдельно каждого звена, а также ЛАХ Lр(w) последовательного соединения.
Рис. 4.2
ЛАХ пропорционального звена L1(w) проходит параллельно оси частот на расстоянии 20lgK1 = 20lg40 = 20lg(10*2*2) = 20дБ + 6дБ + 6дБ = 32дБ.
ЛАХ интегратора L2(w) представляет собой прямую с наклоном -20дБ/дек, которая пересекает ось частот при w = 0.2 рад/с.
Асимптотическая ЛАХ L3(w) апериодического звена с ПФ W3(s) слева от частоты сопряжения 1/T1=1 рад/с проходит параллельно оси частот на расстоянии 20lgK3 = 20lg5 = 20lg(10/2) = 20lg10-20lg2 = 20 дБ-6 дБ = 14 дБ; справа от линии сопряжения имеет наклон -20дБ/дек.
Асимптотическая ЛАХ L4(w) апериодического звена с ПФ W4(s) слева от частоты wс=1/T2=1 рад/с проходит параллельно оси частот на расстоянии 20lgK4 = 20lg(0.25) = 20lg((1/2)*(1/2)) = (-6 дБ)+(-6 дБ) = -12 дБ; справа от линии сопряжения имеет наклон -20дБ/дек.
Сумма этих четырех асимптотических ЛАХ LP(w) представляет собой асимптотическую ЛАХ разомкнутой системы, то есть ЛАХ последо-вательного соединения всех звеньев прямого канала. На рис. 4.2 приведена и уточненная ЛАХ LP(w) (тонкая линия). Максимальное значение поправки dL(wс) = 2*(-3 дБ) = -6 дБ.
Построение ФЧХ. Для пропорционального звена j1(w) = 0 во всем диапазоне частот.
ФЧХ интегрирующего звена j2(w) = -p/2 во всем диапазоне частот.
ФЧХ обоих апериодических звеньев совпадают и имеют значение -p/4 на частоте сопряжения wc = 1/T1 = 1/T2 =1 рад/с.
Результирующая ФЧХ jP(w) для рассматриваемого примера представляет собой смещенную на -p/2 удвоенную характеристику апериодического звена с wc = 1 рад/с. На частоте сопряжения в данном случае имеем фазовый сдвиг jP(wc) = ( -p/2) + 2*(-p/4) = -p.
Предельные соотношения логарифмических частотных характеристик. Влияние вариаций параметров на частотные характеристики соединений звеньев
Предельные соотношения ЛЧХ соедининй звеньев. При построении ЛЧХ последовательного соединения типовых звеньев целесообразно предварительно определить особенности и некоторые параметры ЛЧХ и ФЧХ на низкой частоте (при w ® 0) и на высокой частоте (при w ® ¥). Сделать это можно по виду оператора WP(s):
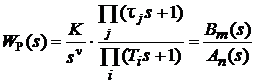 , (4.6)
, (4.6)
где m и n – общие степени полиномов числителя и знаменателя ПФ WP(s), включая интеграторы или дифференциаторы (при их наличии).
Сформулируем следующие правила.
На низкой частоте (при w ® 0):
· Наклон ЛАХ составляет n*(-20 дБ/дек),
· Значение ФЧХ составляет n*(-p/2) рад = n*(-90о).
На высокой частоте (при w ® ¥):
· Наклон ЛАХ составляет (n-m)*(-20 дБ/дек)
· Значение ФЧХ составляет (n-m)*(-p/2) рад = (n-m)*(-90о).
Знание и использование этих правил позволяет сразу наметить асимптотику ЛЧХ соединений типовых звеньев и уменьшить вероятность появления качественных ошибок при построении ЛЧХ.