Интегрирующее звено (интегратор)
Дифферециальное уравнение интегратора
. (3.7)
Передаточная функция представляется в двух видах:
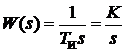, (3.8)
где K=1/TИ. Параметр TИ называется постоянной интегрирования, K - коэффициент передачи или добротность интегратора. Далее будет использоваться запись ПФ интегратора в виде W(s)=K/s .
Подадим на вход интегратора ступенчатое воздействие величины a, т. е. f(t) = a1(t). Изображение такой функции F(s) = a/s. Изображение сигнала на выходе интегратора Y(s) = F(s)W(s) = aK/s2. Обратное преобразование Лапласа дает реакцию интегратора на постоянный сигнал: y(t) = aKt - см. рис. 3.3.
Таким образом, реакция интегратора на постоянное воздействие представляет собой линейно изменяющийся сигнал, тангенс угла наклона которого к оси времени пропорционален величине входного воздействия и коэффициенту передачи интегратора.
Запишем частотный оператор интегрирующего звена:
(3.9)
AЧХ
. (3.10)
Модуль ЛАЧХ (дБ)
. (3.11)
ФЧХ интегрирующего звена
. (3.12)
Рассмотрим АФХ, которая определяется выражением (3.9) – см. рис. 3.4. Все точки АФХ располагаются на отрицательной части оси мнимых. На нулевой частоте интегратор имеет бесконечное усиление; при увеличении частоты модуль ЧХ R(w) в соответствии с (3.10) монотонно уменьшается. Фазовый сдвиг на всех частотах составляет -p/2.
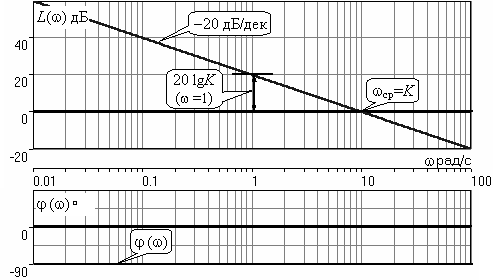
ЛЧХ интегратора строятся по формулам (3.10), (3.11), (3.12) – рис. 3.5.
Рис. 3.5
ЛАХ представляет собой прямую, имеющую наклон –20 дБ/дек; это означает, что при увеличении частоты в 10 раз модуль уменьшается также в 10 раз. Действительно, определим изменение модуля на десятикратном интервале изменения частоты в любом месте частотного диапазона:
DL = L(10wi) - L(wi) = 20lgR(10wi) - 20 lgR(wi) =
= (20lgK - 20lg(10) - 20lg(wi)) - (20lgK - 20 lg(wi)) = –20 дБ .
Для определения местоположения ЛАХ найдем точку её пересечения с осью частот. Данная точка называется частотой среза; при этом имеем R(wср) =1, а L(wср) = 0 дБ. Из (3.10) видно, что R(w) =1 при w = K. Проведенная через эту точку прямая линия с наклоном –20 дБ/дек и является ЛАХ интегратора с коэффициентом передачи K. Найдем еще одну характерную точку при w =1. Из (3.11) следует, что на данной частоте
Прямая, проведенная через эту точку и через точку на оси частот w =K будет иметь наклон –20 дБ/дек. Заметим, что для интегратора с K =1 обе характерные точки совпадают (wср = 1).
ФЧХ интегрирующего звена, как следует из (3.12), представляет собой прямую линию, параллельную оси частот – см. рис. 3.5.
При изменении коэффициента передачи (единственного параметра интегратора) ЛАХ будет смещаться параллельно самой себе: подниматься при увеличении K или опускаться при уменьшении K. Величина смещения ЛАХ DL при изменениии K в DK раз будет составлять DL = 20lg(DK) дБ. Например, при увеличении K в 10 раз ЛАХ поднимется на 20 дБ, а при уменьшении K в 4 раза опуститься на 12 дБ.