Пропорциональное звено
Уравнение имеет следующий видy = Kx. (3.1)
Передаточная функция
W(s) = K/1= K. (3.2)
Описывающее это звено алгебраическое уравнение (3.1) можно рассматривать как вырожденное дифференциальное уравнение нулевого порядка. Во временной области это звено воспроизводит любой входной сигнал, изменяя его величину в K раз. В связи с этим такое звено называется также безынерционным.
Единственный параметр K называется коэффициентом передачи.
Получим частотный оператор звена:
(3.3)
AЧХ пропорционального звена
. (3.4)
Модуль логарифмической ЧХ - ЛАЧХ (размерность в децибеллах (дБ))
(3.5)
ФЧХ определяется выражением
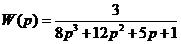О. (3.6)
Рассмотрим АФХ, определяемую выражением (3.3) – см. рис. 3.1.
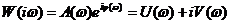Мнимая составляющая ЧХ равна нулю, а вещественная часть равна K и не зависит от частоты. Поэтому траектория конца вектора ЧХ при изменении частоты от нуля до ¥ вырождается в точку.
ЛЧХ определяются выражениями (3.4), (3.5), (3.6) и приведены на рис. 3.2.
 |
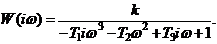ЛАЧХ (часто также используют аббревиатуру “ЛАХ”) представляет собой прямую, параллельную оси частот и проходящую от этой оси на расстоянии 20lgK. Очевидно, что приведенная на рис. 3.2 характеристика построена при значении K = 10.
Рис. 3.2
ФЧХ от параметра K не зависит и совпадает с осью частот.
При K = 0 ЛАХ совпадает с осью частот (20lg1 = 0 дБ); для K< 1 ЛАХ будет проходить под осью частот.
При изменении коэффициента передачи ЛАХ будет подниматься при увеличении K или опускаться при его уменьшении. Величина DL смещения ЛАХ при изменении K в DK раз будет составлять DL = 20lgDK (дБ).
Например, при увеличении K в 2 раза ЛАХ звена поднимется на 6 дБ, а при уменьшении в 2 раза опустится на такую же величину.