Колебательное звено 2-го порядка
Перейти к решению задачиЗвено 2-го порядка может описывать колебательные процессы.
Дифферециальное уравнение звена
. (3.36)
Передаточная функция звена:
, (3.37)
где K - коэффициент передачи, T - постоянная времени. Параметр ζ - коэффициент демпфирования - определяет колебательность процесса.
Корни квадратного уравнения – знаменателя ПФ – определяют вид переходнеого процесса. При ζ > 1 имеем пару разных действительных корней и (3.37) может быть приведено к виду
. (3.38)
В этом случае звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка; реакция на ступенчатое воздействие будет представлять собой апериодический процесс.
При ζ = 1 выражение (3.37) приводится к виду
. (3.39)
Рис. 3.14
В диапазоне значений коэффициента демпфирования 0 < ζ < 1 знаменатель ПФ (характеристический полином звена) имеет пару комплексно-сопряженных корней
(3.40)
Реакция на единичное ступенчатое воздействие будет определяться выражением [2], [4]
, (3.41)
где
. (3.42)
На рис. 3.14 представлены два колебательных процесса для звена с параметрами K =10, T =1 c. при значениях коэффициента демпфирования ζ = 0.15 и ζ = 0.05. Видно, что время окончания процессов определяет огибающая eat. Количество периодов колебаний за время протекания процесса определяется соотношением мнимой и вещественной частей.
На рассматриваемом примере колебательного звена 2-го порядка определим корневые показатели качества процессов в СУ.
h - абсолютное затухание. Определяется как расстояние от мнимой оси до ближайшего корня. Если корень действительный (для рассматриваемого примера это имеет место при ζ ⊃ 1), то h = min|si|. Если ближайшей к мнимой оси оказывается пара комплексно-сопряженных корней si,i+1 = ai ± jwi (для данного примера - при ζ < 1), то h = min|ai|. Абсолютное затухание определяет время окончания переходного процесса – см. рис. 3.14. Значению ζ = 0.15 соответствует пара s1,2 = -0.15 ± j 0.989. Ограничивающая экспонента e-0.15t “давит” колебания до значения ±5% от начального за три своих постоянных времени, что определяет время окончания процесса tp = 3(1/0.15) = 20 c. Для случая ζ = 0.05 имеем пару корней s1,2 = -0.05 ± j 0.999 и tp = 3(1/0.05) = 60 c – см. рис. 3.14.
m - относительное затухание, или колебательность. Определяется как отношение мнимой части к вещественной части той пары комплексно-сопряженных корней, для которой это отношение максимально, т. е. m = max(Imsi / Resi) = max(wi /ai). Относительное затухание характеризует количество периодов колебаний с частотй w, которые “успеют” уложится за время tp. Само значение m приблизительно равно числу экстремумов (т. е. числу полупериодов) процесса за время его протекания tp. Для рассматриваемого примера при ζ = 0.15 имеем m » 6.6 и за время tp = 20 с уложились три полных периода колебаний переходного процесса. При ζ = 0.05 имеем m » 20 и за время tp = 60 с. успели уложится десять периодов.
Рис. 3.15
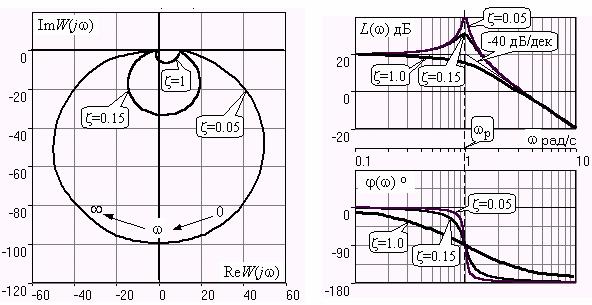
ЛЧХ могут быть построены следующим образом. Сначала строится асимптотическая ЛАХ для значения z=1 - см. рис. 3.15,б. Затем в окрестности частоты сопряжения wс = 1/T вводится поправка, зависящая от величины коэффициента z. Эта поправка может быть взята из таблиц, в которых представлено семейство таких поправок при различных значениях z при изменении частоты w относительно частоты сопряжения wс [3], [4]. В этих таблицах также приводится семейство ФЧХ для разных значений z - см. рис. 3.15,б.
На примере колебательного звена введем также следующие частотные показатели качества СУ.
wр – частота резонанса, на которой имеет место резонанс на ЧХ; с этой круговой частотой и проявляется колебательная составляющая переходного процесса.
M – показатель колебательности (не путать с корневым показателем колебательность или относительное затухание m); определяется по АЧХ:
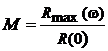. (3.43)
Значение M говорит о числе периодов колебаний за время протекания переходного процесса. Например, для рассматриваемого звена при z=0.15 имеем M=3.36; из рис. 3.14 видно, что за время процесса имют место приблизительно три периода колебаний. При z=0.05 показатель колебательности M=10 и переходный процесс содержит приблизительно десять периодов колебаний на частоте резонанса.