СТАТИСТИЧЕСКИЕ КРИТЕРИИ И ВЫБОР РАСПРЕДЕЛЕНИЯ РИСКА

2.1. Статистические критерии

Вероятность (Р) события (Е) – отношение числа К случаев благоприятных исходов, к общему числу всех возможных исходов (М).

Р(Е)= К / М                                                                                                       (7)

Вероятность наступления события может быть определена объективным или субъективным методом.

Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие. Например, вероятность выпадения «орла» или «решки» при подбрасывании идеальной монеты – 0,5.

Субъективный метод основан на использовании субъективных критериев (суждение оценивающего, его личный опыт, оценка эксперта) и вероятность события в этом случае может быть разной, будучи оцененной разными экспертами.

В связи с этими различиями в подходах необходимо отметить несколько нюансов:

Во-первых, объективные вероятности имеют мало общего с инвестиционными решениями, которые нельзя повторять много раз, тогда как вероятность выпадения «орла» или «решки» равна 0,5 при значительном количестве подбрасываний, а, например, при 6 подбрасываниях может выпасть 5 «орлов» и 1 «решка».

Во-вторых, одни люди склонны переоценивать вероятность наступления неблагоприятных событий и недооценивать вероятность наступления положительных событий, другие наоборот, т.е. по разному реагируют на одну и ту же вероятность (когнитивная психология называет это эффектом контекста).

Однако, несмотря на эти и другие нюансы, считается, что субъективная вероятность обладает теми же математическими свойствами, что и объективная.

Размах вариации (R) – разница между максимальным и минимальным значением фактора

R= X_max - X_min                                                                                                                                                                                        (8)

Этот показатель дает очень грубую оценку риску, т.к. он является абсолютным показателем и зависит только от крайних значений ряда.

Дисперсия – сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности.

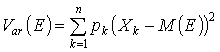,                                                                                                (9)

где М(Е) – среднее или ожидаемое значение (математическое ожидание) дискретной случайной величины Е определяется как сумма произведений ее значений на их вероятности:

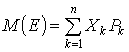.                                                                                                         (10)

Математическое ожидание – важнейшая характеристика случайной величины, т.к. служит центром распределения ее вероятностей. Смысл ее заключается в том, что она показывает наиболее правдоподобное значение фактора.

Использование дисперсии как меры риска не всегда удобно, т.к. размерность ее равна квадрату единицы измерения случайной величины.

На практике результаты анализа более наглядны, если показатель разброса случайной величины выражен в тех же единицах измерения, что и сама случайная величина. Для этих целей используют стандартное (среднее квадратическое) отклонение .

.                                                                                                         (11)

Все вышеперечисленные показатели обладают одним общим недостатком – это абсолютные показатели, значения которых предопределяют абсолютные значения исходного фактора. Гораздо удобней поэтому использовать коэффициент вариации (СV).

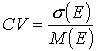.                                                                                                               (12)

Определение CV особенно наглядно для случаев, когда средние величины случайного события существенно различаются.

В отношении оценки риска финансовых активов необходимо сделать три замечания:

Во-первых, при сравнительном анализе финансовых активов в качестве базисного показателя следует брать рентабельность, т.к. значение дохода в абсолютной форме может существенно варьировать.

Во-вторых, основными показателями риска на рынке капиталов являются дисперсия и среднее квадратическое отклонение. Поскольку в качестве базиса для расчета этих показателей берется доходность (рентабельность), критерий относительный и сопоставимый для различных видов активов, нет острой нужды в расчете коэффициента вариации.

В-третьих, иногда в литературе вышеприведенные формулы даются без учёта взвешивания на вероятности. В таком виде они пригодны лишь для ретроспективного анализа.

Кроме того, описанные выше критерии предполагалось применять к нормальному распределению вероятностей. Оно, действительно, широко используется при анализе рисков финансовых операций, т.к. его важнейшие свойства (симметричность распределения относительно средней, ничтожная вероятность больших отклонений случайной величины от центра ее распределения, правило трех сигм) позволяет существенно упростить анализ. Однако не все финансовые операции предполагают нормальное распределение доходов (вопросы выбора распределения рассмотрены более подробно чуть ниже) Например, распределения вероятностей получения доходов от операций с производными финансовыми инструментами (опционами и фьючерсами) часто характеризуется асимметрией (скосом) относительно математического ожидания случайной величины (рис. 1).

Так, например, опцион на покупку ценной бумаги позволяет его владельцу получить прибыль в случае положительной доходности и в то же время избежать убытков в случае отрицательной, т.е. по сути, опцион отсекает распределение доходности в точке, где начинаются потери.

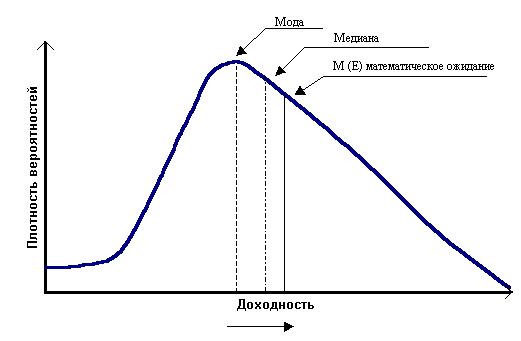
Рис.1 График плотности распределения вероятности с правой (положительной) асимметрией

В подобных случаях использование в процессе анализа только двух параметров (средней и стандартного отклонения) может приводить к неверным выводам. Стандартное отклонение неадекватно характеризует риск при смещенных распределениях, т.к. игнорируется, что большая часть изменчивости приходится на «хорошую» (правую) или «плохую» (левую) сторону ожидаемой доходности. Поэтому при анализе асимметричных распределений используют дополнительный параметр – коэффициент асимметрии (скоса). Он представляет собой нормированную величину третьего центрального момента и определяется по формуле (13):

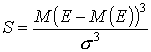.                                                                                          (13)

Экономический смысл коэффициента асимметрии в данном контексте заключается в следующем. Если коэффициент имеет положительное значение (положительный скос), то самые высокие доходы (правый «хвост») считаются более вероятными, чем низкие и наоборот.

Коэффициент асимметрии может также использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равно 0.

В ряде случаев смещенное вправо распределение можно свети к нормальному прибавлением 1 к ожидаемой величине доходности и последующим вычислением натурального логарифма полученного значения. Такое распределение называют логнормальным. Оно используется в финансовом анализе наряду с нормальным.

Некоторые симметричные распределения могут характеризоваться четвертым нормированным центральным моментом – эксцессом (е):

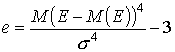.                                                                                               (14)

Если значение эксцесса больше 0, кривая распределения более остроконечна, чем нормальная кривая и наоборот.

Экономический смысл эксцесса заключается в следующем. Если две операции имеют симметричные распределения доходов и одинаковые средние, менее рискованной считается инвестиция с большим эксцессом.

Для нормального распределения эксцесс равен 0.

2.2. Выбор распределения случайной величины

Нормальное распределение используют, когда невозможно точно определить вероятность того, что непрерывная случайная величина принимает какое-то конкретное значение. Нормальное распределение предполагает, что варианты прогнозируемого параметра тяготеют к среднему значению. Значения параметра существенно отличающиеся от среднего, т.е. находящиеся в “хвостах” распределения, имеют малую вероятность осуществления. Такова природа нормального распределения.

Треугольное распределение представляет собой суррогат нормального и предполагает линейно нарастающее по мере приближения к моде распределение.

Трапециевидное распределение предполагает наличие интервала значений с наибольшей вероятностью реализации (НВР) в пределах РВД.

Равномерное распределение выбирается, когда предполагается, что все варианты прогнозируемого показателя имеют одинаковую вероятность реализации

Однако, когда случайная величина дискретна, а не непрерывна, применяют биномиальное распределение и распределение Пуассона.

Иллюстрацией биномиального распределения служит пример с подбрасыванием игральной кости. При этом экспериментатора интересуют вероятности “успеха” (выпадения грани с определенным числом, например, с “шестеркой”) и “неудачи” (выпадение грани с любым другим числом).

Распределение Пуассона применяется, когда выполняются следующие условия:

1.Каждый малый интервал времени может рассматриваться как опыт, результатом которого является одно из двух: либо “успех”, либо его отсутствие – “неудача”. Интервалы столь малы, что может быть только один “успех” в одном интервале, вероятность которого мала и неизменна.

2.Число “успехов” в одном большом интервале не зависит от их числа в другом, т.е. “успехи” беспорядочно разбросаны по временным промежуткам.

3.Среднее число “успехов” постоянно на протяжении всего времени.

Обычно распределение Пуассона иллюстрируют примером регистрации количества дорожных происшествий за неделю на определенном участке дороги.

При определенных условиях распределение Пуассона может быть использовано как аппроксимация биномиального распределения, что особенно удобно когда применение биномиального распределения требует сложных, трудоемких расчетов, отнимающих много времени. Аппроксимация гарантирует приемлемые результаты при выполнении следующих условий:

1.Количество опытов велико, предпочтительно более 30-ти (n=3).

2.Вероятность “успеха” в каждом опыте мала, предпочтительно менее 0.1.(p=0.1) Если вероятность “успеха” велика, то для замены может быть использовано нормальное распределение.

3.Предполагаемое количество “успехов” меньше 5 (np=5).

В случаях, когда биномиальное распределение весьма трудоемко, его также можно аппроксимировать нормальным распределением с “поправкой на непрерывность”, т.е. делая допущение, что, например, значение дискретной случайной величины 2 является значением непрерывной случайной величины на промежутке от 1.5 до 2.5.

Оптимальная аппроксимация достигается при выполнении следующих условий: n=30; np=5, а вероятность “успеха” p=0.1 (оптимальное значение р=0.5)