Контрольная работа по математике

2) Найти dx/dy и для заданных функций: а) y=f(x), б) x=φ(t), y=ψ(t).
а) y=x³lnx; б) x=t-sint, y=t-cost.
Решение. x=t-sint, y=t-cost.
Функция задана в параметрическом виде. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.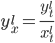

Отдельно находим производные x_t' и y_t'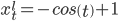


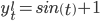
Следовательно: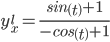

или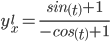

Найдем y_x'' (вторую производную):

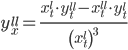
Находим производные x_t'' и y_t''


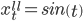
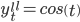
Тогда 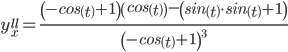или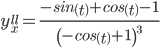

3) Найти наибольшее и наименьшее значение функции y=f(x) на отрезке [a; b].
[0; π/2].
Решение. Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) < 0
то точка x* - локальный (глобальный) максимум. Находим первую производную функции: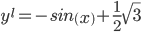

Приравниваем ее к нулю: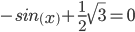

x₁ = ¹/₃•π
Вычисляем значения функции на концах отрезка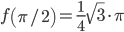

f(0) = 1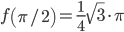

Ответ: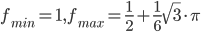

4) Прямоугольник вписан в эллипс с осями 2a и 2b. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?

5) Исследовать методами дифференциального исчисления функцию y=f(x) и, используя результаты исследования, построить ее график.
Y=(x²+1)/(x²-1).