Действительно, так как    и для любых квадратных матриц  A  и     , то

и, следовательно,   и  .
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.
Условие невырожденности матрицы A оказалось не только необходимым для существования ее обратной матрицы, но и достаточным. Т.е. справедлива следующая теорема.
ТЕОРЕМА. Пусть  A – квадратная матрица порядка  .  Матрица  A имеет обратную тогда и только тогда, когда ее определитель  det отличен от нуля. Причем обратная матрица    может быть найдена по формуле:
                                         ,
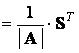где   – матрица из алгебраических дополнений элементов матрицы  A, т.е.
.
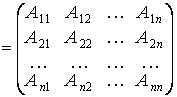Матрица    называется  союзной  (или присоединенной, или взаимной) для матрицы A.
ПРИМЕР. Найти матрицу, обратную к матрице 
.
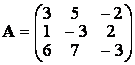Так как определитель матрицы  ,  то матрица имеет обратную. Найдем алгебраические дополнения элементов матрицы A. Получим:
,  ,  ,   
,         ,    ,