,     ,                                                                                   .
Следовательно,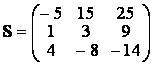
и .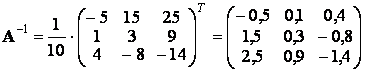
Рассмотрим теперь систему линейных уравнений, в которой число уравнений  n  и число неизвестных  m совпадает и .  Тогда: 
1)   и, следовательно, такая система имеет единственное решение. 
2) Матрица A имеет обратную матрицу .
Покажем, как можно найти решение этой системы с помощью обратной матрицы  .  Запишем систему в матричной форме. Умножим обе части равенства  (2)  на    слева. Получим:
,
,
,
. (3)
Таким образом, если в системе линейных уравнений    и  ,  то система имеет единственное решение, которое можно найти по формуле  (3).  Нахождение решения по формуле  (3)  называют  матричным  методом  решения  системы.