Контрольная работа по математике

2) Составить уравнение касательной плоскости к поверхности z = f(x,y)
z = 3x² – 3xy – 6y, A (4,1), B(3.96; 1.03)
Решение. Запишем уравнения касательной в общем виде:
z - z₀ = f'_x(x₀,y₀,z₀)(x - x₀) + f'_y(x₀,y₀,z₀)(y - y₀)
По условию задачи x₀ = 4, y₀ = 1, тогда z₀ = 30
Найдем частные производные функции z = f(x,y) = 3*x^2-3*x*y-6*y:
f'_x(x,y) = (3•x²-3•x•y-6•y)'_x = 6•x-3•y
f'_x(x,y) = (3•x²-3•x•y-6•y)'_y = -3•x-6
В точке М₀(4,1) значения частных производных:
f'_x(4;1) = 21
f'_y(4;1) = -18
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z - 30 = 21(x - 4) -18(y - 1)
или
-21•x+18•y+z+36 = 0

3) Найти наименьшее и наибольшее значение функции z=f(x;y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
z = 3 – 2x – xy - y

4) Даны функция z = f(x,y), точка A и вектор a. Найти:
grad z в точке A;
производную в точке A по направлению вектора a.
z = ln(5x² – 3y²), A(1;1), a(3;2)
Решение.
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.: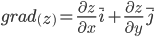

Находим частные производные: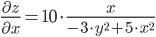


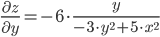
Тогда величина градиента равна: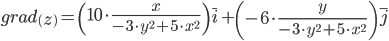

Найдем градиент в точке А(1;1)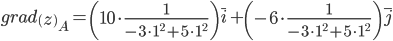

или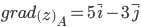

Модуль grad(z):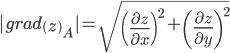


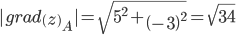
Направление вектора-градиента задаётся его направляющими косинусами: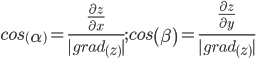


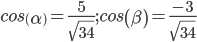
Найдем производную в точке А по направлению вектора а(3;2).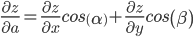

Найти направление вектора - значит найти его направляющие косинусы: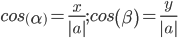

Модуль вектора |a| равен: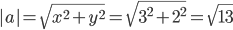

тогда направляющие косинусы: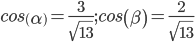

Для вектора a имеем: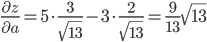

Если ∂z/∂a > 0, то заданная функция в направлении вектора a возрастает.
Если ∂z/∂a < 0, то заданная функция в направлении вектора a убывает.