Аналитическое определение переменных и постоянных затрат
Метод наименьших квадратов. Согласно этому методу, прямая затрат строится таким образом, чтобы сумма квадратов отклонений расстояний от всех точек до теоретической линии регрессии была бы минимальной. Для установления зависимости между затратами и объемом и определения суммы затрат используют методы математической статистики, в частности, метод наименьших квадратов (МНК).
Функция y = а + b∙x, отражающая связь между зависимой и независимой переменными, называется уравнением регрессии, а и b - параметры уравнения.
Применительно к задачам управленческого учета функция Y в этом уравнении - зависимая переменная (общая сумма затрат); а - общая сумма постоянных затрат; b - переменные затраты на единицу продукции; Х - независимая переменная (объем производства).
Метод наименьших квадратов заключается в том, что сумма квадратов отклонений фактических значений функции Y от значений, найденных по уравнению регрессии, должна быть наименьшей или:
∑( yi – y’i)2→ min
где Yi - фактические значения; Y’i - расчетные значения, вычисляемые по заданной формуле.
Для определения параметров уравнения регрессии можно воспользоваться несколькими способами.
Условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Эти уравнения имеют вид:
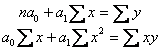
Либо по параболе (квадратическая зависимость 2-го порядка)

В данном случае неизвестные можно найти тремя способами:
| Моменты наблюдения, п | Объем производства (X ) шт. | Общие затраты (Y), т. руб. |
| Январь | 34 | 640 |
| Февраль | 30 | 620 |
| Март | 34 | 620 |
| Апрель | 39 | 590 |
| Май | 42 | 500 |
| Июнь | 32 | 530 |
| Июль | 26 | 500 |
| Август | 26 | 500 |
| Сентябрь | 31 | 530 |
| Октябрь | 35 | 550 |
| Ноябрь | 43 | 580 |
| Декабрь | 48 | 680 |
| Итого | 420 | 6840 |
Требуется определить составляющую переменных и постоянных затрат в структуре общих затрат хозяйствующего субъекта.
Линейная зависимость

Кривая второго порядка
