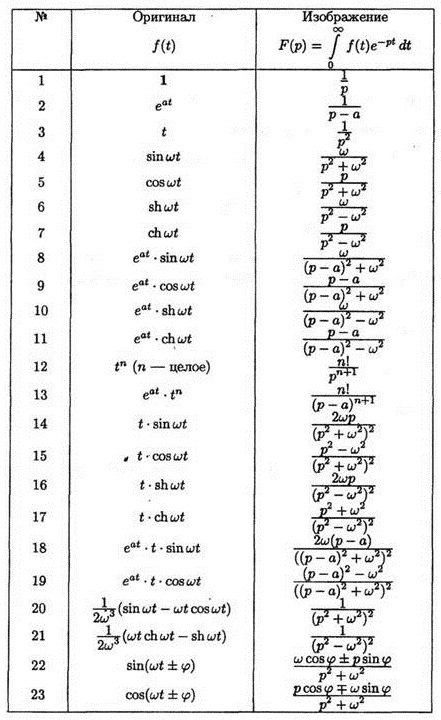
Оригинал и его изображение
Изображением функции f(t) или ее преобразованием Лапласа называется функция F(p) комплексного переменного p, определяемая соотношением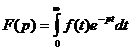
. обозначают F(p) → f(t). Правило получения по заданному оригиналу f(t) изображения F(p) называется преобразованием Лапласа.
Назначение. Данный сервис предназначен для нахождения онлайн оригинала f(t) по изображению F(p). Результаты вычисления оформляются в формате Word (см. пример).
На данный момент все вещественные числа (числа с запятой, например,
0.1 необходимо записывать через дробь, как 1/10)
| Изображение | Оригинал |
| t |
| 1 |
| eat |
| sin(ωt) |
| cos(ωt) |
| e-atsin(ωt) |
| e-atcos(ωt) |
| sh(ωt) |
| ch(ωt) |
Начальной функцией или оригиналом называют функцию f(t) действительной переменной t, удовлетворяющей следующим условиям:
- f(t)=0 при t<0;
- если M>0 и s – некоторые вещественные числа, то |f(t)|≤Mest при t≥0.
- f(t) - кусочно-непрерывная и интегрируемая на любом конечном отрезке изменения t.
Точная нижняя грань s0 всех чисел s, для которых выполняется неравенство, называется показателем роста функции f(t).
Теоремы запаздывания и смещения
Теорема запаздывания: L[f(t-τ)] = e-pτL[f(t)].Пример. e-2p/(p2+1) = η(t-2)sin(t-2)
Теорема смещения: L[ep0tf(t)] = F(p-p0).
Пример. (p+4)/((p+4)2+9) = e-4tcos(3t)