1 |
Системы линейных уравнений
Уравнение называется линейным, если оно содержит неизвестные только в первой степени и не содержит произведений
неизвестных, т.е. если оно имеет вид
![]() ,
,
где ![]() ,
, ![]() – числа.
– числа. ![]() называются коэффициентами уравнения,
называются коэффициентами уравнения, ![]() называется свободным членом. Если
называется свободным членом. Если ![]() , то уравнение называется однородным. В противном случае уравнение называется неоднороным.
, то уравнение называется однородным. В противном случае уравнение называется неоднороным.
В этом параграфе мы будем рассматривать систему ![]() линейных уравнений
с n неизвестными, т.е. систему
вида
линейных уравнений
с n неизвестными, т.е. систему
вида
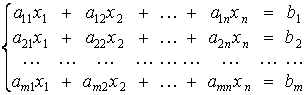 (
1)
(
1)
Обозначим через ![]() и
и ![]() следующие матрицы:
следующие матрицы:
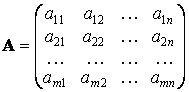 и
и  .
.
Матрицу ![]() называют основной
матрицей системы (1), а матрицу
называют основной
матрицей системы (1), а матрицу ![]() – расширенной матрицей
системы (1).
– расширенной матрицей
системы (1).
Пусть ![]() – матрица-столбец неизвестных, X – матрица-столбец свободных членов, т.е.
– матрица-столбец неизвестных, X – матрица-столбец свободных членов, т.е.
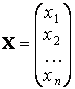 и
и 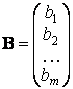 .
.
Тогда систему ( 1) можно записать в виде матричного уравнения ![]() . Его
называют
матричной
формой системы (1).
. Его
называют
матричной
формой системы (1).
Упорядоченный набор чисел ![]() называется решением системы
(1) если он обращает в тождество каждое
уравнение системы. Если система линейных уравнений имеет хотя бы одно решение,
то ее называют совместной. Система линейных уравнений, не имеющая
решений, называется несовместной.
называется решением системы
(1) если он обращает в тождество каждое
уравнение системы. Если система линейных уравнений имеет хотя бы одно решение,
то ее называют совместной. Система линейных уравнений, не имеющая
решений, называется несовместной.