Метод Крамера
1 | 2 |
Теорема. Система из n уравнений с n неизвестными
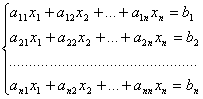
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = ∆i/∆,
где
∆ = det A,
∆i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
|
∆i = |
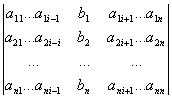 |
Пример
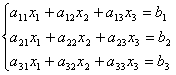
|
A = |
 |
∆1= |
 |
∆2= |
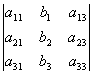 |
∆3= |
 |
x1 = ∆1/detA; x2 = ∆2/detA; x3 = ∆3/detA;