1 | 2 | 3 | 4 | 5 | 6 |
Симплексный метод основан на последовательном переходе от одного базисного решения (опорного плана) задачи линейного программирования к другому опорному плану,
при этом значение целевой функции изменяется в лучшую сторону. Рассмотрим алгоритм симплексного метода на примере решения задачи планирования товарооборота предприятия торговли.
Коммерческое предприятие реализует п товарных групп, располагая т ограниченными материально-денежными ресурсами bi > 0 (i =
1, т). Известны расходы ресурсов каждого i-вида на реализацию
единицы товара по каждой группе, представленной в виде матрицы А = (aij),
и прибыль cj, получаемая предприятием от реализации единицы
товара j-группы (табл. 2.3.1). Необходимо определить объем и структуру
товарооборота хj (j = 1, п), при которых
прибыль коммерческого предприятия была бы максимальной.
Математическую модель задачи запишем следующим образом.
Определить вектор X= (х1, х2,..., xn), который удовлетворяет ограничениям вида
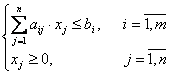
и обеспечивает максимальное значение целевой функции
![]()
Алгоритм симплексного метода включает следующие этапы.
1. Составление первого опорного плана. Система ограничений задачи, решаемой симплексным методом, задана в виде системы неравенств смысла «≤», правые
части которых bi>=0. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных балансовых переменных.
Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:
![]()
где xn+i - дополнительные переменные, i = 1, т,
хj — базисные переменные, j = 1, n.
Решим эту систему относительно дополнительных переменных:
![]()
а функцию цели перепишем в виде уравнения
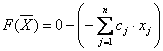
Следует заметить, что опорным решением называется базисное неотрицательное решение.
Полагая, что основные переменные х1 = х2 = x3 =... xn = 0, получим допустимое базисное решение — опорный план Х1 = (0, 0, ... ,0, b1, b2, ... , bm); F(X1) = 0, который заносим в симплексную табл. 2.3.2. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположным знаком.