Проектирование и оценка проекта линейно-угловой сети
Каждый определяемый пункт линейно-углового хода имеет две координаты Х и Y, которые являются неизвестными и которые нужно найти. Общее количество пунктов в ходе
обозначим через п, тогда количество неизвестных будет 2 * ( n - 2 ), так как у
двух пунктов (исходных начального и конечного) координаты известны. Для
нахождения 2 * ( n - 2 ) неизвестных достаточно
выполнить 2 * ( n - 2 ) измерений.
Подсчитаем, сколько измерений выполняется в разомкнутом линейно-угловом ходе: на n пунктах измерено n углов - по одному на каждом пункте, измерены также ( n - 1 ) сторон
хода, всего получается ( 2 * n - 1 ) измерений.
Разность между количеством выполненных измерений и количеством необходимых измерений равна:
(2n-1)-2*(n-2)=3 (12)
то есть, три измерения являются избыточными: это угол на предпоследнем пункте хода, угол на последнем пункте хода и последняя сторона хода. Но тем не менее, эти
измерения
выполнены, и их необходимо использовать при вычислении координат пунктов хода.
В геодезических построениях каждое избыточное измерение порождает какое-либо условие, поэтому количество условий равно количеству избыточных измерений; в
разомкнутом
линейно-угловом ходе должны выполняться три условия: условие, дирекционных
углов и два координатных условия.
Условие дирекционных углов. Вычислим последовательно дирекционные -углы всех сторон хода, используя формулу передачи дирекционного угла на последующую сторону
хода:
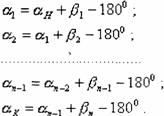 (13)
(13)
Сложим эти равенства и получив:
![]()
откуда
![]()
и
![]() (14)
(14)
Это - математическая запись первого геометрического условия в разомкнутом линейно-угловом ходе. Для правых углов поворота оно запишется так:
![]() (15)
(15)
Сумма углов, подсчитанная по формулам (14) и (15), называется теоретической суммой углов хода. Сумма измеренных углов вследствие ошибок измерений, как правило,
отличается от теоретической суммы на некоторую величину, называемую угловой
невязкой и обозначаемую fβ: