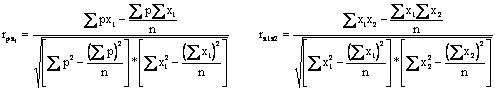1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Суть и обоснование большинства из перечисленных методов подробно изложены в различных учебниках по общей теории статистики (см. ист.4, 14), существуют также пакеты прикладных программ с разработками статистических методов анализа.
Качественная оценка показателей тесноты связи дается, как правило, по шкале Чеддока: слабая связь - 0,1-0,3, умеренная - 0,3-0,5, заметная - 0,5-0,7, высокая - 0,7-0,9, весьма высокая - 0,9-0,99.
На практике для определения тесноты связи двух признаков часто применяется коэффициент ранговой корреляции Спирмена (Р). Значения каждого признака ранжируются по степени возрастания (от 1 до n), затем определяется разница (d) между рангами, соответствующими одному наблюдению.
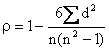
N-число наблюдений (пар рангов).
Широкое применение в анализе цен находят трендовые и регрессионные модели.
Особенностью построения модели зависимости цен от факторов является необходимость выявления мультиколлинеарности (взаимозависимости) факторов и исключения из анализа некоторых из них. Для этого необходимо рассчитать парные коэффициенты корреляции, которые имеют и самостоятельное аналитическое значение (n-число наблюдений):