1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Построение уравнения зависимости цен от факторов осуществляется на основе метода наименьших квадратов (сумма квадратов отклонений фактических данных от выровненных по уравнению должна быть минимальной). Строится система уравнений, при решении которой определяются параметры искомого уравнения. Например, для линейного 3-факторного уравнения регресии (p= a0 + a1 x1 + a2 x2 + a3 x3) система имеет вид:
Для линейной 2-факторной связи в систему подставляем x3= 0, что сокращает число слагаемых в каждом уравнении и уравнений в системе до 3, для 1-факторной модели - x2=0, x3=0, слагаемых и уравнений - по два. Для гиперболы р=a0+a1*, полулогарифмической функции p= a0+a1lgx в систему вместо x подставляем 1/x или lgx соответственно, например:
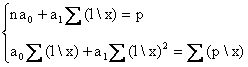
При построении тренда вместо х подставляем t.
На практике же, как правило, используется компьютерный расчет параметров уравнения. На современном рынке существует множество пакетов прикладных программ, в которых заложен перебор различных форм уравнений с учетом их адекватности соответствия реальным данным. Основной критерий адекватности: минимальное значение остаточной дисперсии результативного признака (цены):
где
- отклонения фактических цен от выровненных по формуле.
Чтобы определить, какой из факторов влияет на цену сильнее, рассчитывают стандартизованные показатели (делающие параметры, относящиеся к разным единицам измерения, сопоставимыми):
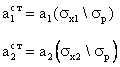
где
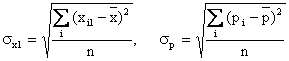- средние квадратические отклонения
факторного и результативного признаков от соответствующих им средних.
Значимость или типичность полученных коэффициентов регрессии проверяется с помощью t-критерия Стьюдента, если исследуемый ряд включает не более 30 уровней, что характерно для ценовых рядов:
где
- среднее квадратическое отклонение
фактических цен от выровненных, для параметра а0 в формуле
отсутствует sх.
Нижний предел значимости (t критическое) определяется по таблице Стьюдента (приводятся в учебниках по общей теории статистики, высшей математике или издаются специально) с учетом принятого уровня значимости a=0,05 и числа степеней свободы n-k (n- число наблюдений, k - число параметров в уравнении).